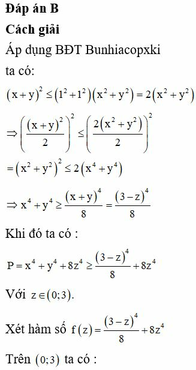Lần sau bạn chú ý dùng chức năng Gõ công thức trực quan để người đọc dễ hiểu để bài nhé. Không hiểu không ai giúp bạn đâu.

Câu hỏi đã được hỏi nhiều lần, có thể xem tại: Cho x,y,z >0 t/m x y z=xyz. C/m \(\dfrac{1 \sqrt{1 x^2}}{x} \dfrac{1 \sqrt{1 y^2}}{y} \dfrac{1 \sqrt{1 z^2}}{z}\le xyz\) - Hoc24

Cho x,y,z là các số nguyên tố khác 2 và các số thực a,b,c thỏa mãn dãy tỉ số bằng nhau a-b/x=b-c/y=a-c/z.CMR a=b=c

Dễ thế mà chẳng ai làm được..

\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2xz+2yz=z^2+\left(x+y\right)^2+2z\left(x+y\right)=36\)

áp dụng BĐT cosi : 

\(z^2+\left(x+y\right)^2\ge2z\left(x+y\right)\)

<=> \(z^2+\left(x+y\right)^2+2z\left(x+y\right)\ge4z\left(x+y\right)=36< =>z\left(x+y\right)\ge9\)

ta lại có \(\dfrac{x+y}{xyz}=\dfrac{x}{xyz}+\dfrac{y}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xz}\) áp dụng BĐT buhihacopxki dạng phân thức => \(\dfrac{1}{yz}+\dfrac{1}{xz}\ge\dfrac{4}{yz+xz}=\dfrac{4}{z\left(x+y\right)}\ge\dfrac{4}{9}\left(đpcm\right)\)

dấu bằng xảy ra khi \(\left[{}\begin{matrix}yz=xz< =>x=y\\x+y+z=6\\z^2=\left(x+y\right)^2\end{matrix}\right.< =>\left[{}\begin{matrix}x+y+z=6\\z=2x=2y\end{matrix}\right.< =>\left[{}\begin{matrix}x=y=\dfrac{3}{2}\\z=3\end{matrix}\right.\)

\(\dfrac{x+y}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xz}\).

Áp dụng bất đẳng thức Cauchy-Schawrz dạng Engel:

\(\dfrac{1}{yz}+\dfrac{1}{xz}\ge\dfrac{4}{z\left(x+y\right)}\)     (1).

Áp dụng bất đẳng thức Cauchy cho hai số dương z và x+y, ta có:

\(z\left(x+y\right)\le\left(\dfrac{x+y+z}{2}\right)^2=9\). Suy ra, \(\dfrac{4}{z\left(x+y\right)}\ge\dfrac{4}{9}\)     (2).

Từ (1) và (2), suy ra \(\dfrac{x+y}{xyz}\ge\dfrac{4}{9}\) (đpcm).

Dấu "=" xảy ra khi và chỉ khi \(\dfrac{1}{yz}=\dfrac{1}{xz}\) và \(z=x+y\).

Vì x,y,z dương nên xyz dương

nên chia cả hai vế của bđt ta được bđt \(\frac{x+y}{xyz}\ge1\)và ta cần chứng minh bđt này đúng thì bđt ban đầu được chứng minh

Ta có \(\frac{x+y}{xyz}=\frac{x}{xyz}+\frac{y}{xyz}=\frac{1}{yz}+\frac{1}{xz}\ge\frac{4}{z\left(x+y\right)}\)( Cauchy-Schwarz dạng Engel ) (*)

Lại có \(z\left(x+y\right)\le\left(\frac{z+x+y}{2}\right)^2=2^2=4\)=> \(\frac{4}{z\left(x+y\right)}\ge\frac{4}{4}=1\)( AM-GM ) (**)

Từ (*) và (**) => \(\frac{x+y}{xyz}=\frac{x}{xyz}+\frac{y}{xyz}=\frac{1}{yz}+\frac{1}{xz}\ge\frac{4}{z\left(x+y\right)}\ge1\)( đpcm )

Vậy bđt ban đầu được chứng minh

Đẳng thức xảy ra <=> \(\hept{\begin{cases}x,y,z>0\\x+y+z=4\\z=x+y\end{cases}}\Rightarrow\hept{\begin{cases}x=y=1\\z=2\end{cases}}\)

M=x+yxy.1z≥2√xyxy.1z=2z√xy≥2z(x+y2)=4z(x+y)M=x+yxy.1z≥2xyxy.1z=2zxy≥2z(x+y2)=4z(x+y)

=4z(1−z)=414−(z−12)2≥16=4z(1−z)=414−(z−12)2≥16

Min M= 16 khi  z=1/2 và  x=y =1/4